«Все всегда идет не по плану» – один из главных принципов, которым стоит руководствоваться при любом планировании. Вспомните, когда в последний раз заранее распланированный день прошел ровно так, как вы и предполагали? Даже если, казалось бы, все форс-мажоры предусмотрены, на деле что-нибудь да произойдет.
Ровно такие же «форс-мажоры» возникают и при решении криптографических задач. Сотни ученых могут годами продумывать все до последней мелочи, но реальность все равно преподнесет сюрприз. Во многом именно бесконечный цикл, состоящий из череды выработки новых криптографических решений, выявления уязвимостей и последующего их устранения так привлекает людей в криптографию.
Например, любопытен эпизод из истории развития всем известного протокола TLS. Первое математическое доказательство безопасности схемы защиты данных, используемой в TLS 1.1, было приведено Кравчиком в 2001 году. Но уже менее чем через год была предложена атака, показавшая нестойкость протокола именно в части защиты данных!
Более детальным расследованием этой захватывающей истории мы займемся во второй части нашей статьи (но, забегая вперед, сообщим, что репутация всеми уважаемого Кравчика в итоге будет полностью восстановлена).
К сожалению, такие казусы не являются чем-то редким в криптографии, а упомянутая выше уязвимость оказалась далеко не последней для многострадального TLS. Каждый год на криптографических конференциях и семинарах представляются новые крайне удивительные атаки, существование которых, на первый взгляд, противоречит теоретическим исследованиям (см. [1, 2, 3]), а фиксы OpenSSL выходят с завидной регулярностью.
И в этот момент возникает вопрос: так в чем же причина «промахов» криптографов-теоретиков? Если теоретические исследования не дают стопроцентных гарантий безопасности, может, и не стоит вообще тратить на них силы и время?
Прежде чем ответить на этот вопрос, давайте попробуем разобраться, на каких столпах стоит криптография, что такое модель противника и каким образом в мире формируется и расширяется знание о таком сложном и многогранном понятии, как «информационная безопасность».
Кто такая Ева?
Разработка систем, решающих задачи обеспечения информационной безопасности, является крайне сложноорганизованным и трудоемким процессом. В действительности оказывается, что теоретические исследования являются только одним из многих этапов жизни таких систем. Не менее важными являются этапы моделирования, реализации и эксплуатации системы, последний из которых является наиболее значимым с точки зрения обычных пользователей. Каждый из этих этапов опирается на предыдущий и является логическим продолжением своего предшественника: например, этап теоретических исследований невозможен без моделирования, ведь строгость рассуждений требует формализации исследуемых свойств и объектов.
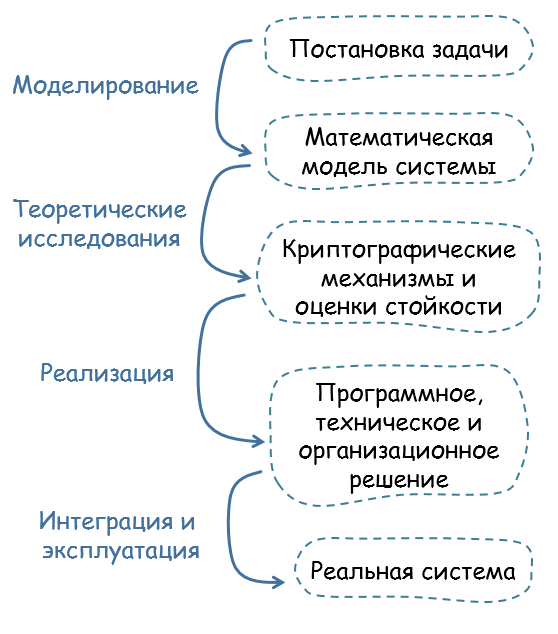
Моделирование в криптографии предполагает глубокий анализ всех свойств разрабатываемой системы, всех возможных способов взаимодействия пользователей с ней, а иногда даже физических условий, в которых система будет функционировать. Результатом моделирования является математическая модель системы, включающая в себя, в частности, так называемую модель противника, которая, на самом деле, и определяет, что значит безопасная или стойкая система.
Модель противника складывается из трех составных частей: тип атаки, модель угрозы и предположения о ресурсах, доступных противнику. Все вместе эти три компоненты позволяют четко определить, в каком мире живет наша система: как противник может с ней общаться, что он может от нее узнать, чего именно хочет достичь и какие ресурсы у него для этого есть.
Тип атаки определяет качественные возможности противника, касающиеся его взаимодействия с анализируемой системой. Так, тип атаки определяет, какую именно информацию о системе противник может получать и каким образом он может вмешиваться в процесс ее работы. Примером является тип атаки, при которой противник может перехватывать и модифицировать данные в канале связи. Здесь возможности противника должны учитывать все известные практические и теоретические методы нарушения безопасности исследуемой системы и быть наиболее приближены к тем, которые возникают при использовании системы на практике.
Модель угрозы определяет задачу по нарушению свойств безопасности, которую стремится решить противник. В качестве примеров можно привести подделку подписи сообщения или компрометацию конфиденциальной информации. В случае решения противником поставленной задачи говорят, что он «реализовал угрозу». Модель угрозы отражает представление о том, какие именно ситуации являются нарушением безопасности конкретной системы.
Предположения о ресурсах противника также являются крайне важной частью модели и определяют теперь уже количественные возможности противника. Обычно они определяются целым набором факторов – временными и вычислительными ресурсами противника, размером его программы, объемом информации, которую он может получить в результате взаимодействия с системой (при этом характер этой информации определяется типом атаки). Без этих ограничений было бы совершенно бессмысленно говорить о безопасности большинства систем, используемых на практике, ведь, например, для них всегда существует противник, который, обладая неограниченными ресурсами, может без применения каких-либо сложных методов найти нужный ключ простым перебором.
Наконец, мы готовы определить, что подразумевается под стойкостью системы. Заметим, что говорить о стойкости системы без привязки к какой-нибудь модели противника совершенно не имеет смысла. Неформально говоря, система называется стойкой в некоторой модели противника, если никакой противник, имеющий определенные моделью возможности и ресурсы, не может реализовать заданную угрозу (то есть вероятность ее реализации достаточно мала).
В реальных условиях
Как только появляется математическая модель исследуемого объекта, возникает возможность применения подходящих математических методов, результаты которых априори являются абсолютно точными (конечно, если автор не наделал ошибок в выкладках и исходные предположения верны). Применение таких методов позволяет выявлять глубинные свойства исследуемого объекта, а при исследовании протяженных во времени процессов, фактически, позволяет предсказывать их будущее. В физике мы предсказываем, за сколько секунд подброшенный вверх камень упадет на землю, а в криптографии – будет ли криптосистема взломана за ближайшие несколько лет. Таким образом, если математическая часть исследований проведена аккуратно и ее результаты не содержат ошибок, то главная причина появления, казалось бы, странных противоречий между теорией и практикой кроется в несоответствии модели противника реальным условиям, в которых система эксплуатировалась на практике.
В таких случаях говорят, что модель оказалась нерелевантной.
При этом, не стоит сразу винить людей, отвечающих за этап моделирования – модель может стать нерелевантной (т.е. недостаточно точно описывающей реальность) на любом этапе процесса разработки системы – от идеи до эксплуатации. При этом расхождения между реальностью и моделью могут появляться в любой из трех частей, составляющих модель. Рассмотрим несколько примеров.
Несоответствие типа атаки
Давайте вернемся к примеру, о котором говорилось во введении, и разберемся, где же произошло расхождение между реальностью и моделью, которую Кравчик использовал в своей работе, и где возникла ошибка, породившая это расхождение.
В той самой работе 2001 года доказывается стойкость схемы аутентифицированного шифрования MAC-then-Encrypt, при которой сначала к сообщению присоединяется его имитовставка, а после конкатенация сообщения и имитовставки шифруется в режиме CBC. Особенность режима шифрования CBC в том, что он умеет обрабатывать только строки, которые можно разделить на блоки некоторого фиксированного размера. Поэтому для того, чтобы можно было обрабатывать сообщения любой длины, обычно применяется процедура дополнения (padding): после добавления к сообщению имитовставки получившаяся строка дополняется до необходимого размера по определенному правилу. При обработке сообщения на принимающей стороне сначала осуществляется расшифрование и проверка корректности дополнения, а уже потом проверяется имитовставка.
Меньше чем через год после публикации работы Кравчика была представлена атака padding oracle attack на режим CBC. Она использует возможность получения противником информации о том, возникла ли на принимающей стороне ошибка при проверке дополнения у расшифрованного сообщения. Результатом атаки является нарушение конфиденциальности передаваемых данных. Подробнее об этой атаке можно прочитать здесь и в статьях нашего блога. Первое время считалось, что протокол TLS защищен от padding oracle attack, так как ошибки в нем возвращаются только в зашифрованном виде и поэтому ошибка в дополнении неотличима от ошибки в имитовставке. Однако криптоаналитикам удалось установить, что для большинства реализаций время выдачи ошибки в случае неверного дополнения отличается от времени выдачи других ошибок, так как в случае неправильного дополнения ошибка выдается сразу, и никакие действия далее не проводятся. Эта разница во времени позволила различить ошибки, возвращаемые принимающей стороной, и применить padding oracle attack к протоколу TLS.
В модели Кравчика, однако, не учтено, что противник может получать информацию о том, где конкретно произошла ошибка при расшифровании. Это упущение привело к несоответствию типа атаки реальным возможностям противника, которых оказалось больше, чем предполагала модель. Такие возможности появились ввиду особенностей функционирования системы (порядка обработки ошибок), возникших на этапе ее реализации.
Таким образом, вся ситуация, поначалу бросившая тень на работу всеми уважаемого ученого, оказалась далеко не такой ужасной: доказательство Кравчика было абсолютно верным, просто модель, в которой оно проводилось, стала нерелевантной.
Несоответствие модели угрозы
Не менее интересны уязвимости, возникающие из-за несоответствия модели угрозы. Они появляются, если некоторые возможные ситуации не были расценены как негативные. Одним из примеров такой уязвимости является возможность восстановить примерную транскрипцию зашифрованного VoIP-разговора, зная только длины зашифрованных пакетов. Первоначально считалось, что наличие этой информации у противника не представляет большую угрозу по нарушению конфиденциальности и в лучшем случае может раскрыть язык разговора или наличие определенных фраз. Но ученые из университета Северной Каролины установили, что при совместном использовании определенных способов кодирования голосовой информации и поточных шифров, сохраняющих длину сообщения, при помощи компьютерной лингвистики и статистических методов возможно достаточно точно воссоздать транскрипцию всего разговора. Таким образом, ошибка в определении угрозы закралась на самом этапе моделирования. Так как система создавалась для шифрования именно голосовых звонков, такая угроза могла быть замечена уже на начальном этапе разработки криптографического протокола.
Несоответствие предположений о ресурсах противника
Атака Sweet32, в свою очередь, основана на уязвимости, возникающей из-за несоответствия предположений о ресурсах противника. Атака Sweet32 приводит к нарушению конфиденциальности и направлена на режим шифрования CBC, использующий блочные шифры с небольшой длиной блока, например, шифр 3DES или Blowfish с длиной блока 64 бита. Эта атака основана на парадоксе дней рождения и для успешного проведения требует, чтобы соединение с сервером поддерживалось на протяжении порядка 38 часов для отправки около 785 ГБ трафика (на практике секретное значение cookie удалось восстановить даже быстрее – за 30 часов и 610 ГБ).
При этом еще в 2000 году была опубликована работа, в которой уже приводилась зависимость вероятности взлома режима CBC от количества зашифрованных данных. В те далекие времена даже при использовании 64-битного блочного шифра зашифрование такого объема данных, которого было бы достаточно для взлома режима CBC, являлось в реальности неосуществимым. Поэтому и режим CBC на основе 64-битного блочного шифра считался стойким на практике. Однако со временем ресурсы, требующиеся для осуществления Sweet32, перестали быть фантастическими. Это просто не было замечено, и на этапе эксплуатации появилось несоответствие между моделью и реальностью. Таким образом, на практике ресурсы, доступные противнику, оказались существенно больше, чем это предполагалось в модели.
Следуя Дарвину
Стоит заметить, что после появления публикаций о каждой из уязвимостей, описанных в рассмотренных примерах, сразу же принимались меры по их устранению. Это общая практика для совершенно любой уязвимости, обнаруженной в системе. Появляются работы, в которых исследуются способы устранить проблему вплоть до прекращения использования уязвимых или даже потенциально уязвимых решений (например, в TLS 1.3 режим CBC не используется), появляются обновленные практические реализации систем. Однако при условии безошибочных теоретических исследований найденные уязвимости запускают и другой не менее важный процесс: анализ несоответствия модели противника реальным условиям и ее последующее расширение, которое будет использоваться уже в рамках нового витка теоретических исследований. Такой процесс, по сути, представляет собой эволюцию модели противника.
Таким образом, в реальности разработка системы – это замкнутый цикл, при котором после интеграции решений идет не менее важный процесс эксплуатации, тоже вносящий свои коррективы. В процессе эксплуатации наши знания о возможностях противника и свойствах безопасности могут значительно расширяться, причем иногда в результате взлома системы по итогам сторонних или внутренних исследований. Такие «открытия» запускают новую итерацию жизненного цикла системы.
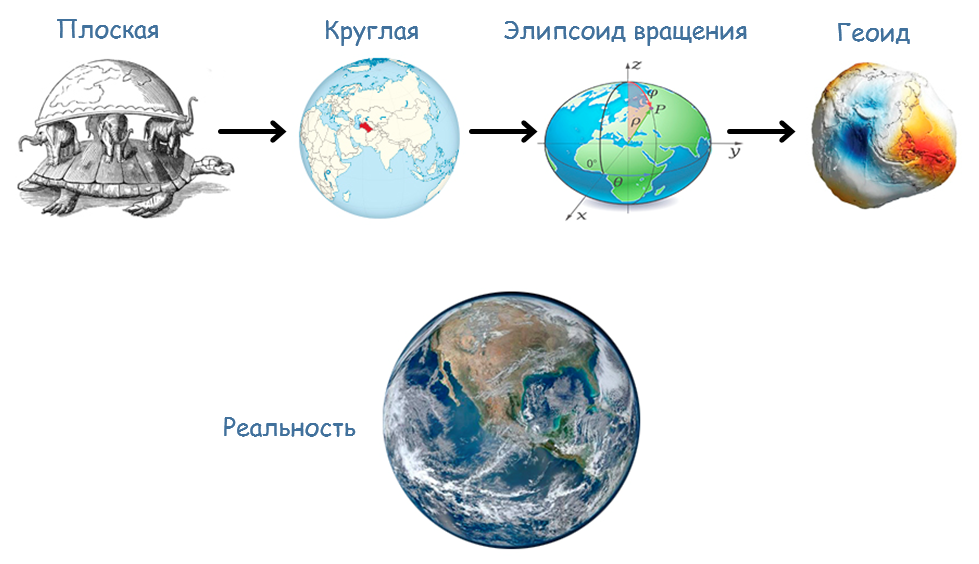
Но не стоит относиться к такому порядку разработки как к чему-то страшному и считать ее цикличность признаком несовершенства процесса. Криптография не отличается от других наук – аналогичная ситуация встречается повсеместно. Лишь одним из примеров является развитие представления людей о форме Земли как одной из самых осязаемых и доступных широкому пониманию моделей. Эта модель претерпела эволюцию от модели плоской Земли до модели Земли как шара, затем эллипсоида вращения, а уже после геоида, постепенно отвечая на все новые вопросы человечества: "Почему существует горизонт, за которым ничего не видно?", "Почему по одной траектории доплыть быстрее, чем по другой?" и т.д. В данном случае появление эффекта, который не согласуется с предсказаниями теории, является аналогом взлома теоретически стойкой криптосистемы на практике. Таким образом, теоретические исследования в самых полных на текущий момент моделях противника (и учет их результатов при разработке реальной системы) позволяют увеличить вероятность того, что в случае взлома системы найденная уязвимость углубит наше понимание аспектов информационной безопасности в целом.
Стоит также отметить, что теоретические исследования позволяют предугадать многие атаки прежде, чем они будут реализованы на практике. Например, в 1997 году было показано, что использование режима CBC с предсказуемым инициализирующим вектором является небезопасным. Однако никаких изменений в реализацию протоколов, использующих такой способ шифрования, внесено не было, так как предложенная атака казалась чересчур теоретической. К 2011 году, несмотря на большое количество исследований, предупреждавших о возможности такой атаки на TLS, уязвимость так и не была устранена, и криптоаналитики представили практическую реализацию атаки, получившую название BEAST (о которой также было написано в нашем блоге). Только тогда уязвимость была закрыта.
В заключение отметим, что каждый этап разработки системы важен и должен взаимодействовать с предыдущими этапами, «прислушиваясь» к их результатам. Такой процесс обеспечивает именно эволюцию знаний, а не простое «латание дыр». Поэтому так важно не пропускать никакой из этапов и уделять должное внимание разработке новых моделей и теоретическим исследованиям.
Алексеев Е.К.
Ахметзянова Л.Р.
Божко А.А.
Смышляева Е.С.
