В данной статье мы затронем сферу защиты информации, которая в последнее время массово обсуждается на всех уровнях – от газетных статей с кричащими заголовками до узкоспециализированных форумов и серьезных научных публикаций. Речь пойдет о слабостях, намеренно внесенных в системы защиты информации – закладках.

Немного о терминологии и классификации

Слабости в криптосхемах, о которых пойдет речь в данной заметке, обычно называют “закладками”. Термин “закладка” (имеющий, как может показаться, несколько сленговый оттенок) зафиксирован в РФ на самом высоком уровне (ГОСТ Р 51275-99, см. [1]):

программная закладка: Внесенные в программное обеспечение функциональные объекты, которые при определенных условиях (входных данных) инициируют выполнение не описанных в документации функций программного обеспечения, позволяющих осуществлять несанкционированные воздействия на информацию;

Несмотря на многочисленные примеры предположительных случаев внедрения программных и аппаратных закладок, практически ни один из источников не дает четких ответов на вопросы о точных механизмах их функционирования. Ниже мы рассказываем о некоторых возможных сценариях, которые могут использоваться для того, чтобы получать доступ к колоссальному объему зашифрованных данных во всем мире, используя ошибки и скрытые уязвимости в криптографических алгоритмах и протоколах. Существует множество вариантов классификации скрытых уязвимостей, приведем один из них:

1. Дефекты, ошибки реализации (bugs) – непреднамеренные ошибки в реализации криптографических систем.
2. Багдоры (bugdoors = bugs & backdoors) – преднамеренная ошибка в программной реализации, которая может выглядеть как непреднамеренная. Обычно в таких ошибках легко отрицать наличие злого умысла.
3. Закладки (backdoors):

• Алгоритмические закладки – преднамеренное скрытое искажение части алгоритма программы, в результате которого возможно появление у программного компонента функций, не предусмотренных спецификацией;
• Аппаратные закладки – электронные устройства/микросхемы, скрытно внедряемые в элементы атакуемой информационной системы;
• Программные закладки – внесенные в программное обеспечение функциональные объекты, которые при определенных условиях инициируют выполнение не описанных в документации функций.

Вне зависимости от способа внедрения, функционирования и воздействия на атакуемую систему, все эти уязвимости так или иначе могут быть использованы для осуществления несанкционированного воздействия на информацию.

Основное внимание в данной статье уделяется именно тем случаям, когда появление уязвимости в системе можно объяснить преднамеренными действиями с чьей-то стороны. Самая большая проблема, связанная с такими уязвимостями, заключается в том, что они крайне трудно детектируются. Чем “глубже” уровень встраивания закладки или багдора, тем сложнее их обнаружить. Закладки, внедренные на этапе производства, практически не поддаются никаким методам выявления, а большинство примеров их обнаружения основываются на чистой удаче.

Фиксирование слабых параметров Диффи-Хеллмана или как АНБ следит за пользователями

В 2012 году Джеймс Бамфорд, ссылаясь на анонимные источники,  опубликовал статью, в которой говорится о том, что Агентство Национальной Безопасности (АНБ) добилось “вычислительных прорывов”, давших возможность взламывать текущие криптографические системы с открытым ключом. Годом позднее в своих заявлениях Эдвард Сноуден затронул ту же проблему, рассказав о созданной АНБ программе разведки PRISM, позволяющей дешифровывать значительную часть перехваченного интернет-трафика.

Однако ни одно из этих заявлений не давало ответов на вопрос, как АНБ это делает, что вызвало обширные дискуссии в интернет-сообществе на тему бэкдоров и закладок в широко используемых криптографических алгоритмах.

Еще в 1990-x годах был разработан алгоритм факторизации целых чисел под названием “метод решета числового поля” или, как принято называть его в англоязычной литературе, NFS-метод (number field sieve) [3]. Для криптографии он был интересен тем, что позволил (это сделала группа учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США) успешно получить доступ к данным, зашифрованным при помощи 768-битного ключа RSA [4]. Существовали также работы, описывающие способы применения данного подхода к задаче дискретного логарифмирования (см., например, [5]). Такие алгоритмы требуют больше времени по сравнению с факторизацией модулей RSA, что не позволяет применять их для практически интересных размеров параметров. Однако эффективность этих алгоритмов можно повысить за счет предварительных вычислений, хоть и очень трудоемких. Это и сделали четырнадцать криптографов, которые осенью 2015 года опубликовали статью [20], в которой NFS-метод, использующий результаты предвычислений, был успешно применен для решения задачи дискретного логарифмирования и атаки на процедуру Диффи-Хеллмана.

Применяемый в работе NFS-метод дает возможность для любой фиксированной мультипликативной группы конечного поля вычетов (по сути – для любого простого числа p) провести процедуру предвычислений, позволяющую в дальнейшем быстро получать любой конкретный дискретный логарифм для каждого конкретного элемента в этой группе (то есть решать относительно x уравнение g^x = y mod p для любого элемента y из группы). Это предоставляет возможность доступа к вырабатываемому в рамках процедуры Диффи-Хеллмана секрету. Так, недельные предвычисления для одного 512-битового простого числа p дали возможность находить конкретный дискретный логарифм в соответствующей группе всего за одну минуту.

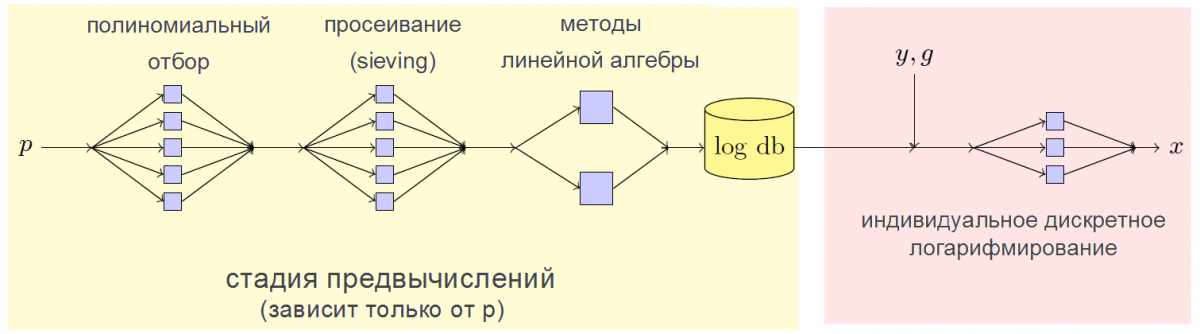
Стоит отметить, что NFS-метод не накладывает никаких дополнительных ограничений на число p, а значит применим к любым, даже рекомендованным “стойким” группам. Более того, его также можно применять и к числам большей размерности, однако на это потребуется гораздо больше вычислительных ресурсов. В частности, необходимо несколько миллионов долларов, чтобы создать суперкомпьютер, который за один год полностью выполнит процедуру предвычислений для одного конкретного числа p наиболее часто используемой при защите пользовательской информации длины 1024 бита.

Авторы статьи обращают внимание на то, что, по данным Сноудена, неофициальный бюджет АНБ составляет порядка $ 10 млрд в год, где более чем $ 1 млрд уходит на эксплуатацию компьютерной сети. Учитывая это, агентству не составляет труда осуществлять настолько дорогостоящие операции.

Трудозатраты колоссальны, можно подумать, ведь простых чисел размерности 512 бит, а тем более 768 и 1024 бита огромное количество. Однако в ходе анализа популярных интернет-протоколов оказалось, что на текущий момент функционируют миллионы серверов, использующих одни и те же группы.

Во многих реализациях простые числа либо зашиты в код, либо постоянно переиспользуются одни и те же наборы рекомендованных безопасных простых чисел. В качестве примера подобных наборов можно привести так называемые группы Оукли: (Oakley Group 1 (768 bit), Oakley Group 2 (1024 bit), Oakley Group 5 (1536 bit)). Подобные рекомендации создавались для того, чтобы исключить возможность использования “слабых” групп, к которым применимы различные известные методы быстрого нахождения дискретного логарифма. Другая причина – желание противостоять UKS-методам (в частности, используются в атаке на TLS TLS triple handshake), заключающимся в возможности нарушителя поддерживать несколько соединений на одном ключе – в частности, в случае мультипликативных групп полей вычетов это возможно делать, подбирая параметры группы. В большей части HTTPS (TLS), IPsec и SSH-соединений используются меньше десятка простых чисел.

Таким образом, цель оправдывает средства. Предвычисление, выполненное для одного из простых чисел, позволит проводить пассивный перехват сообщений 18% сайтов с поддержкой HTTPS, а для другого позволит дешифровывать трафик 66% IPsec VPN-соединений и 26% SSH-серверов. Подобные затраты на вычисления одного модуля являются, таким образом, более чем разумной инвестицией для государственных спецслужб. Сами исследователи сравнивают данный случай с «криптоанализом Энигмы во время Второй Мировой».

Генерация неповторяющихся простых чисел в процедуре Диффи-Хеллмана не гарантирует защиты от атак с использованием NFS-метода, если длины параметров малы. В качестве примера можно привести уязвимость TLS под названием Logjam, связанную с навязыванием наборов шифрования DHE_EXPORT и использования при согласовании ключей мультипликативных групп полей по 512-битовому модулю.

Таким образом, становится возможным существенно понижать стойкость протокола. Проделав предвычисления для наиболее распространенных простых 512-битных чисел, злоумышленник может получить возможность в режиме реального времени взламывать TLS-соединения, оставаясь незамеченным.

Хотя на подобное пока нет прямых улик, применение предвычислений для ускорения взлома процедуры Диффи-Хеллмана при использовании фиксированных 1024-битовых модулей – это вполне правдоподобная теория, объясняющая, каким образом может функционировать программа PRISM.

А все ли хорошо с генераторами случайности?

Качественные случайные и псевдослучайные последовательности играют огромную роль при использовании криптографических средств, и зачастую от них полностью зависит стойкость системы. Можно привести следующие примеры случаев, в которых использование плохого источника случайности приводит к краху безопасности всей системы:

• использование одного и того же значения в качестве случайного параметра в алгоритмах подписи DSA, ECDSA, ГОСТ Р 34.10-94, ГОСТ Р 34.10-2001, ГОСТ Р 34.10-2012 при обработке двух разных сообщений на одном ключе позволяет восстановить секретные ключи подписи и подделывать подпись. Подобная ошибка в реализации ECDSA была успешно использована при обходе защиты в Sony PlayStation 3;
• Использование одного и того же случайного набора в качестве синхропосылки (IV) поточных шифров или блочных шифров, работающих в режимах CFB или гаммирования, приводит к перекрытию гаммы и к возможности восстановления частей открытого текста. Подобное уже случалось в реальных системах – неправильное использование шифра RC4 позволяло восстановить части документов MS Word и Excel по последовательности автосохраненных копий (см. [6]).

Одним из требований к генератору случайных и псевдослучайных чисел является непредсказуемость – то есть невозможность по некоторому выходному отрезку последовательности узнать, какая псевдослучайная последовательность будет на выходе генератора в дальнейшем. Это требование очень важно не только в теории, но и на практике, так как секретные данные (ключи схемы) и открытые синхропосылки обычно генерируются одним и тем же генератором без переинициализации, что дает возможность злоумышленнику знать фрагменты его выхода заранее.

Архитектура современных генераторов случайных чисел

Типичная архитектура генератора случайных последовательности состоит из двух частей: источника “настоящей” энтропии TRNG (True Random Number Generator) и детерминированного генератора DRBG (Deterministic Random Number Generator). Разделение на два компонента обусловлено тем, что TRNG обычно работает медленно и не всегда дает возможность качественно проконтролировать корректность его работы. Второй слой DRBG работает гораздо быстрее, так как является детерминированным генератором, в основе которого лежит определенный алгоритм, принимающий на вход начальное значение (seed) и разворачивающий его в длинную псевдослучайную последовательность с заранее определенными свойствами. Под детерминированностью генератора подразумевается то, что начальное значение всегда разворачивается в одну и ту же последовательность. От того, насколько сложно по выходу этого слоя восстановить начальное значение и внутреннее состояние генератора, зависит стойкость системы.

Рассмотрим теперь несколько примеров, показывающих, как закладки могут быть внедрены в генераторы случайных чисел.

Dual_EC_DRBG

Dual_EC_DRBG – детерминированный генератор псевдослучайных последовательностей, который был разработан специалистами АНБ и после некоторых изменений был стандартизирован NIST. Некоторое время спустя Фергюсон и Шумов заметили, что при знании определенных секретных свойств констант, определяющих генератор, по его выходу можно определить последовательности, которые он выдаст в процессе дальнейшей работе. Пожалуй, среди известных этот случай является самым близким к тому, что можно назвать алгоритмической закладкой, – огромное количество обстоятельств указывает на намеренное продвижение АНБ этого генератора со специальными фиксированными константами в NIST.

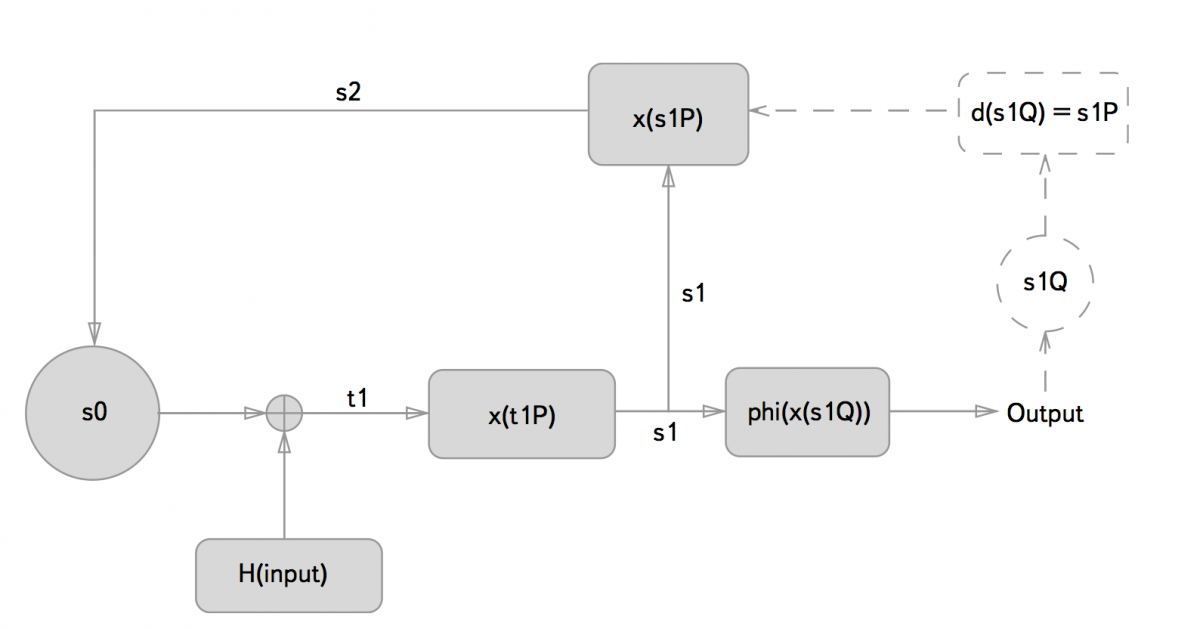
Следует отметить следующие любопытные моменты. Во-первых, если внимательно присмотреться к схеме работы, то видно, что знание соотношения между точками P и Q, то есть знание такого d, что P=dQ, позволяет, наблюдая один полный блок выхода (30 байт), восстановить внутреннее состояние генератора, при условии отсутствия дополнительного ввода (Additional Input). Принцип работы данной закладки изображен на схеме пунктиром. Во-вторых, в 2005 году несколько членов комитета по стандартизации подали заявку на патент, в котором была описана схема генератора Dual_EC_DRBG и пример его использования для депонирования ключей (key escrow). В-третьих, параметры для данного генератора были выбраны сотрудниками АНБ, при их генерации не использовался принцип “проверяемой случайности” и они вошли в нормативное представление стандарта, то есть были обязательны к использованию, а не просто служили для проверки корректности реализации.

Intel Secure Key

Технология генерации случайных чисел Intel Secure Key, также известная как Bull Mountain, была разработана исследовательским центром Intel’s Circuit Research Lab и внедрена в процессоры, начиная с архитектуры Ivy Bridge. Она содержала две инструкции процессора –  RDSEED и RDRAND, опирающиеся на аппаратные источники энтропии (по крайней мере, так заявляют разработчики Intel). Первая функция генерирует начальное значение для датчика псевдослучайной последовательности, вторая – является тем самым генератором DRBG, который выдает блок псевдослучайных данных, используя результат работы RDSEED.

Некоторая информация о том, как этот функционал реализован в процессорах, есть в документации Intel [7]. В общих чертах алгоритм работы описывается следующим образом: две пары чисел по 256 бит, полученных из аппаратного источника энтропии, передаются в аппаратный блок, выполняющий криптографический алгоритм AES в режиме выработки имитовставки AES-CBC-MAC.

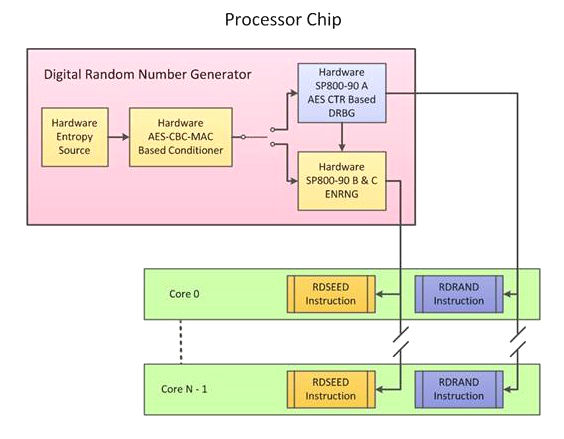
Разработчики Intel утверждали, что данные инструкции обладали хорошими статистическими свойствами и работали достаточно быстро. Однако в свете недавнего скандала с внедрением бэкдора АНБ в Dual_EC_DRBG, описанного нами в предыдущем разделе, многие подозревали Bull Mountain в наличии тех или иных закладок. Так, к примеру, бывший разработчик ядра Linux утверждал, что ушел с работы из-за внедрения в их ДСЧ-модуль  инструкции RDRAND от Intel.

В ответ на эти заявления создатель ядра Linux Линус Торвальдс высказал достаточно резкий довод в пользу безопасности своего продукта: “Краткий ответ: мы знаем, что мы делаем. Вы – нет. Развернутый ответ: мы используем RDRAND как один из многих источников входных данных в пуле случайных чисел и мы используем его для повышения случайности этого набора. Так что даже если в RDRAND есть бэкдор от АНБ, наш способ использования RDRAND в реальности улучшает качество набора случайных чисел, который вы получаете из /dev/random”.

Однако в 2013 году Тейлор Хорнби представил прототип реализации инструкции RDRAND для внедрения закладки в работу устройства /dev/random в ядре Linux.

Если скачать версию 3.12.8 кода ядра Linux, то в файле drivers/char/random.c можно найти функцию extract_buf(), которая используется при чтении из /dev/random. Ниже приведен фрагмент её кода:

    for (i = 0; i < LONGS(EXTRACT_SIZE); i++) {

               unsigned long v;

               // arch_get_random is RDRAND.

               if (!arch_get_random_long(&v))

                       break;

               hash.l[i] ^= v;

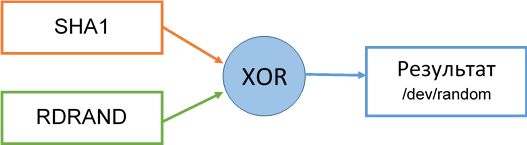
Казалось бы, Линус Торвальдс был совершенно прав в своих заявлениях, ведь даже если предположить, что RDRAND в процессе работы выдает плохую предсказуемую последовательность, качественный энтропийный пул, выработанный ранее и использующийся в функции хэширования, компенсирует данную уязвимость.

По словам Хорнби, данная схема является стойкой только в теории, на практике же во время выполнения инструкции RDRAND хэш-значение находится в памяти компьютера и с большой вероятностью в кэше процессора, а, значит, на этапе своей работы RDRAND может (в обход официальным инструкциям своей работы) в качестве выходного значения взять, например, инвертированное значение хэша. Для того, чтобы вырабатываемая последовательность казалась случайной, конечно, нужно будет использовать более сложно устроенную функцию от хэша, чем простое инвертирование. Для реализации данного подхода необходимо лишь получить доступ к регистру, указывающему на область стека, в которой хранится это хэш-значение.

Используя Bochs (эмулятор процессора), Хорнби представил реализацию инструкции RDRAND на языке C++, код доступен любому желающему.

Некоторые исследователи считают, что такой механизм довольно сложно реализовать на практике, работать он будет долго и гораздо проще сделать так, чтобы инструкция RDRAND использовала алгоритм шифрования AES с ключом, известным только разработчикам закладки. В этом случае устройство /dev/random не пострадает, но атаке могут быть подвержены те приложения, которые используют результаты работы RDRAND напрямую, что поощряется разработчиками процессора (например, комментарий David Johnson из Intel).

Исходя из документации Intel, один вызов инструкции RDRAND занимает 150 тактов, чего в целом достаточно для осуществления подобной атаки и затруднения определения наличия закладки по времени исполнения.

Факт, что некоторый функционал в процессорах Intel реализован при помощи обновляемого микрокода, добавляет еще больше подозрений, так как закладка может быть внедрена в определенную партию процессоров на этапе производства либо же вместе с обновлением микрокода.

Далее рассматривается необычный пример того, как использование "плохой случайности" может приводить к появлению ключей, которые представляют опасность друг для друга.

Как плохая случайность постепенно и незаметно "убивает" RSA

Основная идея взлома алгоритма RSA, использованного совместно с плохим генератором случайных чисел, основана на вычислениях наибольших общих делителей (НОД) используемых модулей. Предположим, нам даны два модуля RSA N₁ = p₁·q₁ и N₂ = p₂·q₂, являющиеся произведением двух простых чисел. Если они имеют один общий простой множитель (далее разделенный множитель) p₁ = p₂ = p, то, посчитав НОД(N₁, N₂), мы получим значение p, а значит легко решим задачу факторизации обоих ключей, найдя их делители. Простые числа, произведение которых является модулем RSA, генерируются в соответствии с некоторой процедурой, включающей генерацию случайных чисел. Если несколько серверов использовали для этого плохие генераторы, то вероятность совпадения одного из сомножителей у двух модулей RSA сильно возрастает. Поскольку модуль RSA является частью открытого ключа, у злоумышленника есть возможность создать базу этих модулей, обработать ее и взломать с помощью указанного выше метода часть RSA-ключей.

Из теоремы о распределении простых чисел следует, что существует порядка 10¹⁵¹ простых чисел размерности 512 бит. Даже если взять миллиарды случайно сгенерированных модулей RSA, шанс встретить нетривиальный НОД крайне мал.

Однако в реальности множители, произведение которых является модулем RSA, генерируются далеко не всегда чисто случайными. Более того, одно и то же простое число p зачастую повторяется множество раз. В статье [8], опубликованной лабораторией Ленстры, авторы собрали обширную базу доступных ключей и сертификатов. Проанализировав её, ученые пришли к выводу, что из тысячи проверенных модулей RSA в среднем два являются небезопасными. Был создан специальный сервис, позволяющий всем пользователям проверить свои модули.

Немного позднее команда ученых из колледжа Ройял Холлоуэй Лондонского Университета провела исследования (см. [9]), в ходе которых в общедоступных сетях были найдены большие кластеры слабых модулей RSA, имеющих общие множители. Один простой множитель встречался 28394 раза, еще два – более 1000 раз, а в общей сложности 1176 множителей повторялись 100 или более раз каждый. По данным ученых, возникновение множителя, повторяющегося более чем 28000 раз, было связано с широкополосным маршрутизатором с модулем SSL VPN – другими словами, можно говорить об ошибке  или, возможно, преднамеренном багдоре реализации, в которой генерировалось одно число и вшивалось в устройство.

Подобные цифры дали более чем серьезные основания для поиска уязвимостей, связанных с разделением общего простого множителя в модулях RSA. Однако размер реальных баз модулей варьируется от 10⁶ до 10¹³ элементов. Это приводит к тому, что время обработки данных становится недопустимо большим, и даже при использовании самых быстрых реализаций алгоритма нахождения НОД двух чисел для нахождения НОД всех пар модулей средствами пользовательской вычислительной машины для некоторых баз требуется около 30 лет.

Однако существует ряд более эффективных методов (см. [10]), направленных на обработку больших массивов модулей RSA. Их применение дает возможность решать подобные задачи с помощью ресурсов обычной лаборатории, не говоря уже о возможностях государственных структур.

Вывод из этих данных по-прежнему можно вынести следующий: ни один стойкий алгоритм не обеспечит пользователям нужного уровня безопасности, если в нем некорректно генерируются или используются его параметры.

Заключение или как от всего этого защититься

Как же избежать внедрения закладок? Помимо очевидных рекомендаций по соблюдению всех требований к эксплуатации криптосредств (например, по корректной настройке датчиков случайных чисел) приведем несколько принципов, которые позволяют защититься хотя бы от части известных на сегодняшний день методов внедрения алгоритмических закладок (или убедиться, что закладок нет):

• Использовать проверенные группы. Необходимо понимать, что не все циклические группы одинаково безопасны – например, в группе чисел {0,...,n-1} с операцией сложения по модулю n задача дискретного логарифмирования решается тривиальным делением, которое выполняется почти мгновенно. С учетом того, что было описано в начале данной статьи, использование мультипликативной группы конечного простого поля также вызывает определенные опасения. На сегодняшний день наиболее надежными в плане не только задачи дискретного логарифмирования, но и других важных задач (вычислительной и распознавательной задач Диффи-Хеллмана) представляются группы точек эллиптических кривых, определенных над простым конечным полем, выбранных с учетом требований стойкости ко всем существующим методам криптоанализа (см., например, [2] и [15]).
• Если фиксировать “подозрительные” группы, то хотя бы большие. При использовании (и уж тем более при стандартизации) криптографических параметров необходимо учитывать не только существующие на сегодняшний день методы криптоанализа, но и учитывать тенденцию к увеличению мощности вычислительной техники и развитию известных методов. Так, более или менее стойким с учетом некоторой перспективы может считаться модуль RSA длиной от 3072 бит (см. [11]). При этом считается, что примерно тем же уровнем стойкости обладает группа точек эллиптической кривой мощности от 2²⁵⁶ (то есть 256 бит).
• Использовать решения без скрытых элементов структуры. Закладки, наподобие той, которая была обнаружена в датчике Dual_EC_DRBG, показывают важность использования принципа “доказуемой псевдослучайности” при порождении тех или иных криптографических параметров. Это означает, что помимо предъявления конкретных значений, создатели спецификации должны описать процедуру, с помощью которого эти значения были получены. При этом принципы построения данного алгоритма должны быть ясны и понятны.

Отметим, что в России не стандартизированы криптосистемы, основанные на задаче дискретного логарифмирования в кольцах вычетов (к которым относится и RSA), а от использования простых полей при подписи и выработке ключей отказались еще в 2001 году [12]. На данный момент в РФ стандарт электронной подписи предполагает использование групп точек эллиптических кривых над полями размера 256 и 512 бит. Принцип доказуемой псевдослучайности стал де-факто обязательным к применению для отечественных специалистов. Так, он использовался (см. [13]) при выработке параметров алгоритма Стрибог, принятого в качестве стандарта функции хэширования [14]. Также данный принцип  используется при выработке параметров алгоритмов, фиксирующихся в качестве рекомендаций по стандартизации Технического комитета по стандартизации "Криптографическая защита информации" (ТК 26) (см., например, [15] и [2]). Подробно о том, как вырабатывались параметры эллиптических кривых, рассказано в статьях [16] и [17], опубликованных ранее в нашем блоге. Что касается скрытого перехода на работу со слабыми параметрами по аналогии с атакой Logjam, то для отечественных протокольных решений это невозможно, т.к. в них просто нет слабых параметров. Все параметры протокола TLS выбраны таким образом, чтобы обеспечивать стойкость с большим запасом (см. [18] и [19]).

В заключение отметим следующее немаловажное обстоятельство. Ответ на вопрос, является ли та или иная слабость схемы намеренно привнесенной, во многом зависит от того, насколько отвечающий на этот вопрос является сторонником теории заговора. Поэтому окончательное суждение о том, является ли та или иная слабость закладкой (то есть, заложена ли она намеренно), читатель должен вынести сам.

Авторы выражают благодарность Мошниной Д.А. и Николаеву В.Д. за ценные замечания и конструктивную критику.

Литература

[1] ГОСТ Р 51275-99 «Защита информации. Объект информатизации. Факторы, воздействующие на информацию. Общие положения».

[2] Информационная технология. Криптографическая защита информации. Рекомендации по стандартизации. Задание параметров эллиптических кривых в соответствии с ГОСТ Р 34.10-2012. http://www.tc26.ru/methods/recommendation/%D0%A2%D0%9A26%D0%AD%D0%9A.pdf

[3] J.P. Buhler, Jr. H.W. Lenstra, and Carl Pomerance. Factoring integer with the number field sieve. In "The development of the number field sieve", volume 1554 of Lecture Notes in Mathematics. pages 50–94. Springer–Verlag, 1993. http://link.springer.com/chapter/10.1007%2FBFb0091539

[4] Kleinjung T., Aoki K., Franke J., Lenstra A.K., Thome E., Bos J.W., Gaudry P., Kruppa A., Montgomery P.L, Osvik D.A., Herman te Riele, Timofeev A., Zimmermann P. Factorization of a 768-bit RSA modulus. https://eprint.iacr.org/2010/006.pdf.

[5] Gordon D. Discrete Logarithms in GF(p) using the number field sieve, SIAM J Discrete Math. 6 (1993), 124-138. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.106.8844&rep=rep1&type=pdf

[6] Hongjun Wu, The Misuse of RC4 in Microsoft Word and Excel. https://eprint.iacr.org/2005/007.pdf

[7] Intel Digital Random Number Generator (DRNG), Software Implementation Guide, Revision 1.1, August 7, 2012. https://software.intel.com/sites/default/files/m/d/4/1/d/8/441_Intel_R__DRNG_Software_Implementation_Guide_final_Aug7.pdf

[8] Lenstra A.K., Hughes J.P., Augier M., Bos J.W., Kleinjung T., Wachter C. Ron was wrong, Whit is right. http://infoscience.epfl.ch/record/174943/files/eprint.pdf

[9] Albrecht M.R., Papini D., Paterson K.G. and Villanueva-Polanco R., Factoring 512-bit RSA Moduli for Fun (and a Profit of $9,000). https://martinralbrecht.files.wordpress.com/2015/03/freak-scan1.pdf

[10] Cloostermans B. Quasi-linear GCD computation and factoring RSA moduli. Eindhoven: Technische Universiteit Eindhoven, 2012. http://alexandria.tue.nl/extra1/afstversl/wsk-i/cloostermans2012.pdf

[11] NIST Special Publication 800-57 Recommendation for Key Management – Part 1: General – Barker E., Barker W., Burr W., Polk W., Smid M., Gallagher P.D., Under Secretary For 2012. http://csrc.nist.gov/publications/nistpubs/800-57/sp800-57_part1_rev3_general.pdf 

[12] Информационные технологии. Криптографическая защита информации. Процессы формирования и проверки цифровой подписи. ГОСТ Р 34.10-2001, Государственный Стандарт Российской Федерации.

[13] Рудской В.И. Об алгоритме выработки констант функции хэширования «Стрибог». https://www.tc26.ru/ISO_IEC/Streebog/streebog_constants_rus.pdf

[14] ГОСТ Р 34.11-2012. Информационная технология. Криптографическая защита информации. Функция хэширования.

[15] Информационная технология. Криптографическая защита информации. Рекомендации по стандартизации. Задание параметров скрученных эллиптических кривых Эдвардса. http://www.tc26.ru/methods/recommendation/CPECC14-TC26.pdf

[16] Смышляев С.В., Ошкин И.Б., Алексеев Е.К., Сонина Л.А. Скрученные эллиптические кривые Эдвардса: когда, зачем, для кого? http://www.cryptopro.ru/blog/2014/12/04/skruchennye-ellipticheskie-krivye-edvardsa-kogda-zachem-dlya-kogo

[17] Смышляев С.В. Эллиптические кривые для нового стандарта электронной подписи. http://www.cryptopro.ru/blog/2014/01/21/ellipticheskie-krivye-dlya-novogo-standarta-elektronnoi-podpisi

[18] Смышляев С.В., Алексеев Е.К. Методические рекомендации ТК 26: алгоритмы, сертификаты, CMS, TLS. http://www.cryptopro.ru/blog/2014/07/07/metodicheskie-rekomendatsii-tk-26-algoritmy-sertifikaty-cms-tls

[19] Информационная технология. Криптографическая защита информации. Рекомендации по стандартизации. Использование наборов алгоритмов шифрования на основе ГОСТ 28147-89 для протокола безопасности транспортного уровня (TLS). http://www.tc26.ru/methods/recommendation/%D0%A2%D0%9A26TLS.pdf

[20] Adrian D., Bhargavan K., Durumeric Z., Gaudry P., Green M., Halderman J.A., Heninger N., Springall D., Thome E., Valenta L., VanderSloot B., Wustrow E., Zanella-Béguelin S., Zimmermann P. Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. https://weakdh.org/imperfect-forward-secrecy-ccs15.pdf

 

Смышляев С.В.

ООО "КРИПТО-ПРО"

Алексеев Е.К.

ООО "КРИПТО-ПРО"

Грибоедова Е.С.,

ООО "КРИПТО-ПРО"

 

Сидоров Е.С.,

независимый эксперт